转子振动的基本特性

　　旋转机械的主要部件是转子，其结构型式虽然多种多样，但对一些简单的旋转机械来说，为分析和计算方便，一般都将转子的力学模型简化为一圆盘装在一无质量的弹性转轴上，转轴两端由刚性的轴承及轴承座支承。该模型称为刚性支承的转子，对它进行分析计算所得到的概念和结论用于简单的旋转机械是适用的。由于做了上述种种简化，若把得到的分析结果用于较为复杂的旋转机械时不够精确，但基本上能够说明转子振动的基本特性。

　　大多数情况下，旋转机械的转子轴心线是水平的，转子的两个支承点在同一水平线上。设转子上的圆盘位于转子两支点的中央，当转子静止时，由于圆盘的重量使转子轴弯曲变形产生静挠度，即静变形。此时，由于静变形较小，对转子运动的影响不显著，可以忽略不计，即认为圆盘的几何中心O′与轴线AB上O点相重合，如图1-1所示。转子开始转动后，由于离心力的作用，转子产生动挠度。此时，转子有两种运动：一种是转子的自身转，即圆盘绕其轴线AO′B的转动;另一种是弓形转动，即弯曲的轴心线AO′B与轴承联线AOB组成的平面绕AB轴线的转动。

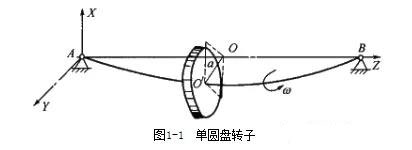
　   盘的质量以m表示，它所受的力是转子的弹性力F，

　　F=-ka

　　式中，k为转子的刚度系数，a=OO′。圆盘的运动微分方程为

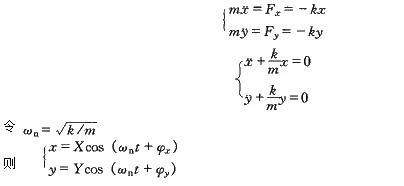
　　式中，X、Y为振动幅度;φx、φy为相位。

　　由上式可知，圆盘或转子的中心O′，在互相垂直的两个方向作频率为ωn 的简谐振动。在一般情况下，振幅X、Y不相等，O′点的轨迹为一椭圆。O′的这种运动是一种“涡动”或称“进动”。转子的涡动方向与转子的转动角速度ω同向时，称为正进动;与ω反方向时，称为反进动。