回路电阻测试仪常见故障及处理方式

　　回路电阻测试仪常见故障及回路电阻测试仪故障处理方式，在电力系统中，为了确保回路电阻测试仪的有效、准确测量，根据以下故障和产生的原因采取相应的解决方式对故障进行处理。因此，回路电阻测试仪在使用的过程中经常会遇到各种故障影响仪器的正常测量。

　　***先，由于交流电源没有接通或没有安装保险管，以及熔断，因此，当回路电阻测试仪与220V交流电源相接入的时候，风机就会发生毫无运转的迹象，即使在按下测试开关的时候，各表也毫无显示。同时，在没有将回路电流接好或测试开关没有闭合的情况下，当测试开关按下以后，电流表没有显示，但是微欧表的******位上却显示为1。因此，在测试之前要对回路电阻测试仪进行详细检查和排除。例如：检查测试线、闭合测试开关、重接和夹电源。其次，由于电压夹位置与实际电压夹位置不符和所测电阻值超过规定范围，电压信号出现未接通或断线的情况，即使测试电流正常，但是微欧表的******位上却显示为1，同时，过低的电源电压、电源线和测试线夹接触不良、C1和C2线柱松动等问题，导致直流输入压降过大，无法满足190V，出现回路电阻测试输出的电流不到100A。因此，可以通过采用合格电源和电源线，对电压信号回路和被测

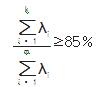
　　由此确定载荷矩阵：A=(e1i，e2i，……eki)T

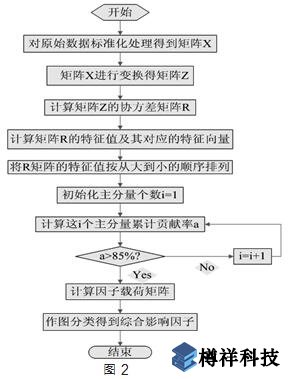
　　3)回路电阻测试仪主成分分析简化雅克比矩阵：

　　由于Cross法的不合理之处是对雅克比矩阵的过度简化，我们运用主成分分析的理论对Cross法改进措施是对雅克比矩阵的合理简化，环的原有分支流量在每一个主成分上的载荷系数有大有小，对于一个特定的主成分而言，某个分支在该主成分上的载荷系数越大说明该主成分主要解释该分支的流量，因此，对于一个特定的主成分，我们可以根据载荷系数的大小，舍去其解释不显著的分支，这样便可对传统的雅克比矩阵合理的化简。主成分分析对雅克比矩阵化简的具体步骤为：

　　①余枝流量与环分支的关联矩阵D(G)的建立对任一个余枝构成的环路确定一个矩阵D(G)=(dij)(N-J+1)×n(r)，矩阵的列数等于该环路的分支数n(r)，矩阵的行数为余枝的个数。由于环路的每一个分支流量可以化为余枝流量的线性叠加，因此矩阵元素dij便是余枝流量在该分支的贡献率即线性叠加系数：

　　②主成分的更新

　　根据环r原有的分支在主成分上的载荷系数的大小，舍去解释信息不显著的分支。新的主成分为载荷系数较大的分支与其对应的载荷系数乘积的线性组合。

　　③环的结构重构

　　将这k个主成分作为环r的分支，对原有的环进行结构重构，于是环r的分支数减少为k个，这k个分支的流量为原有分支流量的线性叠加。由此确定载荷矩阵：A=(e1i，e2i，……eki)T

　　④重构环各支路流量的确定

　　由于重构环的每一个支路各对应一个主成分，对于某一个特定的主成分i(i=1～k)，若其解释原有m条环支路流量Qj(j=1～m)，则该支路的流量可通过下式确定：

　　⑤重构环各支路阻抗的确定

　　该支路的阻抗可以通过当量压头损失求得：

　　⑥雅克比矩阵的化简

　　由牛顿法可知，环r(r=1～N-J+1)，对应得确定雅克比矩阵的第r行元素。对于原有的余枝流量Qj(j=1～M)，从重构环r中找到含有Qj线性组合项的支路，并编号为1～n(n≤k)，则雅克比矩阵的第r行对应Qj的元素可以根据复合求导法则得出即：